分布定数回路と集中定数回路の関係を無限等比級数で読み解く (2)

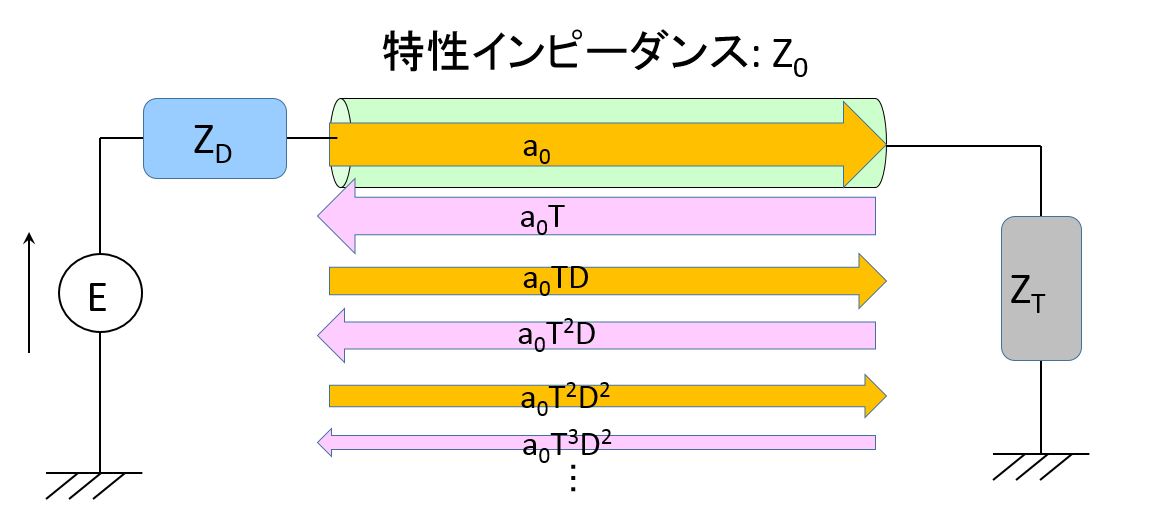
分布定数回路(1)の続きです。
比が1未満の場合の無限等比級数の和の公式は、
$\frac{a_{0}}{1-r}$
ですね。
ですので、オレンジの矢印の総和は、

$\frac{a_{0}}{1-TD}=\frac{Z_{0}+Z_{T}}{2\left(Z_{T}+Z_{D}\right)}E$
ここで、
$\ a_{0}=\frac{Z_{0}}{Z_{0}+Z_{D}}E$
$\ TD=\frac{Z_{T}-Z_{0}}{Z_{0}+Z_{T}}*\frac{Z_{D}-Z_{0}}{Z_{0}+Z_{D}}$

ピンクの矢印の総和は、
$\frac{a_{0}T}{1-TD}=\frac{Z_{T}-Z_{0}}{2\left(Z_{T}+Z_{D}\right)}E$

そして最後に、
オレンジ矢印の総和とピンク矢印の総和を足し算すると、
$\ V_{0}=\frac{Z_{0}+Z_{T}}{2\left(Z_{T}+Z_{D}\right)}E+\frac{Z_{T}-Z_{0}}{2\left(Z_{T}+Z_{D}\right)}E$
$\ = \frac{Z_{T}}{Z_{D}+Z_{T}}E$
となります。

つまり、$\ V_{0} $が最終的に辿り着く値は、$\ V_{0}= \frac{Z_{T}}{Z_{D}+Z_{T}}E$
です。
$\ Z_{0}$ が含まれていませんね。
かつ、下図の普通のオームの法則の答えに辿り着きましたね。

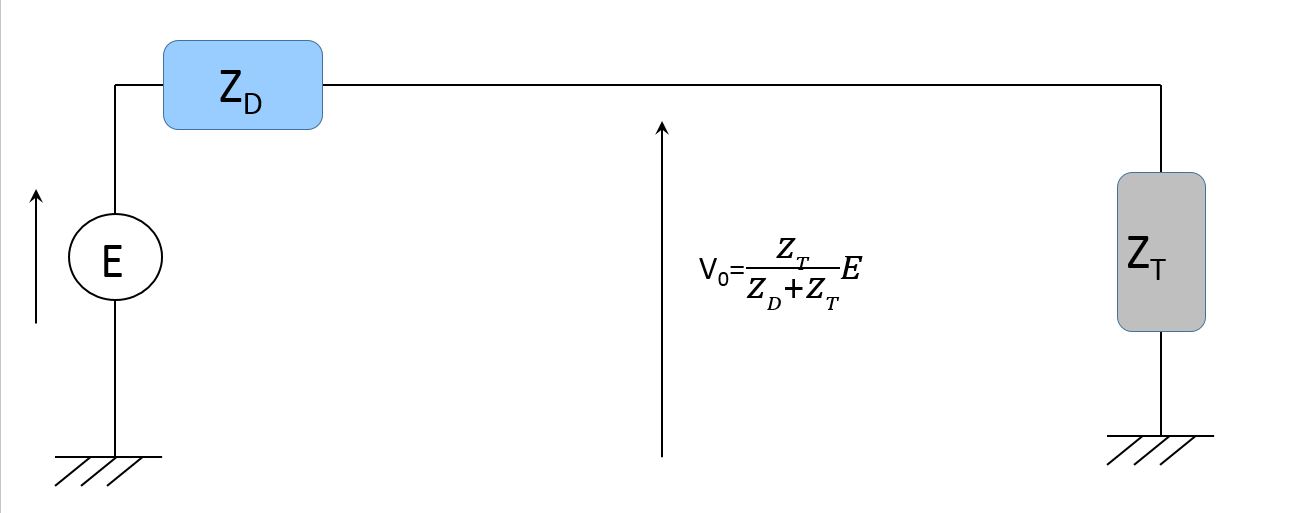
これが何を意味するか。
そう。
伝送路に現れる電圧は、特性インピーダンスに関わらず、
最終的には、集中定数回路でみたオームの法則の解に収束する。