メーカーや専門商社にいると、
「高調波」といった言葉を時々聞くと思います。
特にアンプの特性を語るとき、よく使われる
わけですが、高調波は、どこからともなく
やって来るわけではありません。
出力波形の歪を周波数の世界で表現すると、
「高調波成分が乗る」わけですが、
今回は、それの超簡単な解説を試みます。
アンプの特性と出力波形
特にアンプの特性を
議論するとき、
必ずと言っていいほど、
「高調波成分」という
言葉がでてきます。
理想のアンプは、
入力波形をそのままの形で、
出力レベルのみ一定の比率で
増幅(若しくは縮小)して
出力します。
ただし、
現実のアンプでは、
出力波形に歪みが生じます。
これが、高調波成分を生み出す
のですが、
波形の歪みと周波数成分に
どういう関係があるのか。
それを以下に、解説を試みます。
あるアンプへの入力が、
周波数: $\ f_{0} $
の理想のサイン波だったとします。
その場合、
アンプからの出力の理想は、
$\ A\sin \omega_{0}t$ (図1)
※ $\ \omega_{0}=2\pi f_{0} $
この場合、入力の周波数は、$\ f_{0} $
出力の周波数も$\ f_{0}$ です。
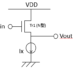
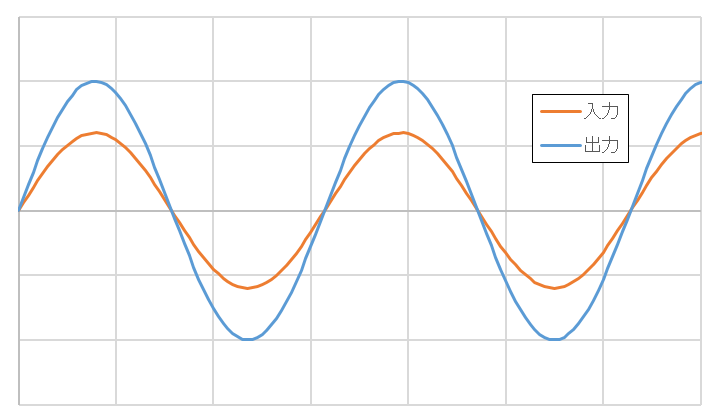図1 理想の出力波形しかし、
現実のアンプは、
(好ましくない)特性を
持ちますので、
出力波形に歪みが生じます。
例えば、
出力レベルの限界により
歪んだ出力波形は、
図2のようになります。
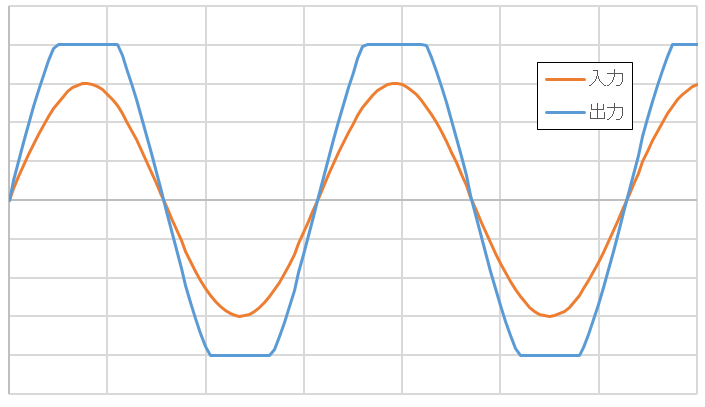図2 歪のある出力波形それでは、
これらの出力波形の周波数成分を
求めてみましょう。
出力波形の周波数成分を求める
出力波形の周波数成分を
求める手法として、
フーリエ級数展開があります。
フーリエ級数展開のコンセプトは、
ある周波数($\ f_{0}$)の任意の関数: $\ D(t)$は、
式(1)のように表される。
$\ D(t)=\frac{a_{0}}{2}+\sum^{\infty}_{n=1}(a_{n}\cos n\omega_{0} t+b_{n}\sin n\omega_{0} t)$ ・・・式(1)
※ $\ \omega_{0}=2\pi f_{0} $
すなわち、周波数:$\ f_{0}$の任意の関数$\ D(t)$は、
$\ f_{0}$の整数倍の周波数のサイン波/コサイン波
の足し算で表されます。
さて、図2の出力波形ですが、
波形に歪みがあるものの、
周波数: $\ f_{0}$の
任意の関数の一つです。
つまり、
フーリエ級数展開が適用できます。
図1の理想の出力波形にも、
もちろんフーリエ級数展開は
適用できます。
この場合、式(1)の$\ b_{1}$のみ有限の値で、
他の$\ a_{n}$, $\ b_{n}$ は、ゼロとなります。
つまり、$\ f_{0}$以外の
周波数成分はゼロとなります。
しかし、
図2の出力波形については、
式(1)の$\ b_{1}$ 以外の$\ a_{n}$, $\ b_{n}$も、
何らかの有限の値となります。
つまり、
$\ f_{0}$の整数倍の周波数成分が
発生します。
高調波成分とは？
つまり、
図1の理想の出力は、
入力の周波数:$\ f_{0}$以外の
周波数成分がないのに対して、
図2の出力波形は、
入力の周波数: $\ f_{0}$の整数倍の
周波数成分も含みます。
これを「高調波成分」と呼びます。
以上。
補足
$\ a_{n}, b_{n}$の具体的な求め方や、
フーリエ級数展開に関する詳細は、
下記のサイトが分かりやすいです。
(拙者も忘れかけていたのを
このサイトで再度勉強しました。)
http://www7b.biglobe.ne.jp/~yizawa/InfSys1/basic/chap3/index.htm
また、
フーリエ級数展開や
信号解析について
本でじっくりと
勉強されたい場合は、
下記書籍も
よろしかったら、
手に取っていただければ
と思います。
