エンジニア生活
をしていると、時々、
「Sパラメータ」
というものに
出くわします。
知っている人は
よく知っているのですが、
意外と知らない人も多い。
「今更、他人に聞きづらい。」
という人もいると思います。
ここでは、それを、
こっそりお教えしましょう。
Sパラメータ(以下Sパラ)は、
下記のような行列で表されます。
$\left(\begin{array}{cc} S_{11}&S_{12} \\S_{21}&S_{22}\end{array}\right)$
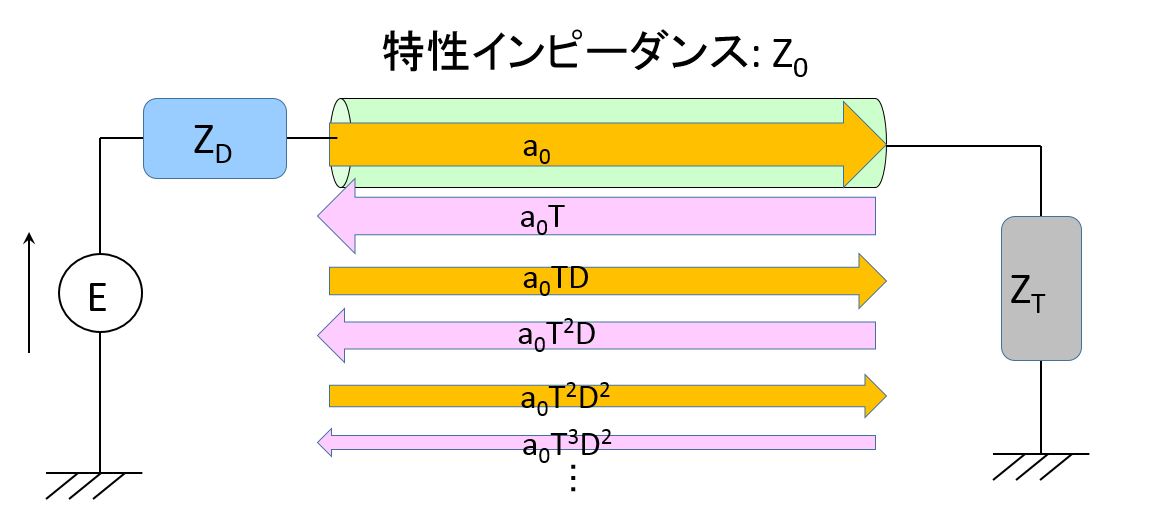
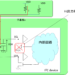
Sパラを使用する場合は、
下図のような
系を想定します。
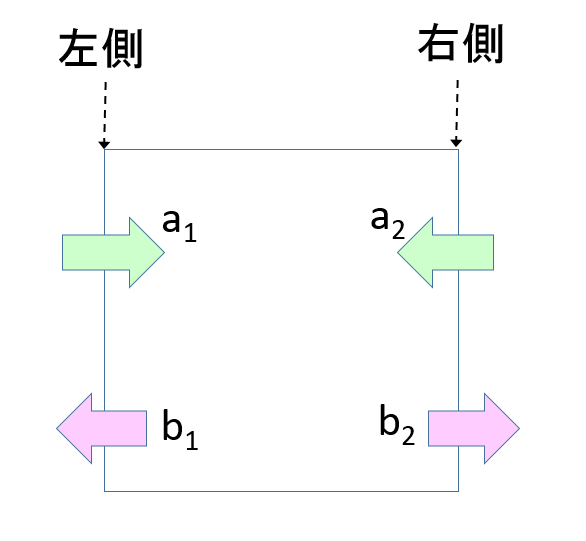
左側に入力される波動
(電波でも音波でも良い。)
を$\ a_{1}$ 、
右側に入力される波動を
$\ a_{2}$ とします。
そして、
左側から出力される波動を $\ b_{1}$
右側から出力される波動を $\ b_{2}$
とします。
出力される波動は、
何らかの入力の結果であり、
$\ b_{1}$は、$\ a_{1}$の入力が
右側で反射して戻ってきたものと、
$\ a_{2}$の入力が減衰(若しくは増幅)して
伝わってきたものを
重ね合わせた
ものと考えます。
また、$\ b_{2}$は、
$\ a_{1}$の入力が減衰(若しくは増幅)
して伝わってきたものと、
$\ a_{2}$の入力が左側で反射して
戻ってきたものを
重ね合わせたもの
と考えます。
これを
上記のsパラを使用して
表現すると
以下のようになります。
$\left(\begin{array}{c} b_{1}\\b_{2}\end{array}\right)
=
\left(\begin{array}{cc} S_{11}&S_{12} \\S_{21}&S_{22}\end{array}\right)
\left(\begin{array}{c} a_{1}\\a_{2}\end{array}\right)$
上記を展開すると、
$\ b_{1}=S_{11}*a_{1} + S_{12}*a_{2} $
$\ b_{2}=S_{21}*a_{1} + S_{22}*a_{2} $
$\ S_{11}$ と$\ S_{22}$ を反射係数、
$\ S_{12}$ と$\ S_{21}$ を透過(または増幅)係数
とすると、
上記の波動の
重ね合わせの考え方と一致します。
これがSパラメータです。
A8.netが技術スタッフを募集中