こんにちは。
今日は、
分布定数回路について.
「反射」とか、「透過」と聞いただけで、
アレルギーを起こすエンジニアを時々、
見かけます。
他の事は優秀なのにもったいない。


余計なお節介かもしれませんが、
以下、ヘーシロー。が分布定数回路について、
解説します。
分布定数回路と集中定数回路はどう違うのか?
結果的には同じものです。
「結果的には」といったのは、
分布定数回路には、
「過程」が含まれるからです。
(集中定数回路でもAC信号を扱い、過渡応答のような
ものは「過程」にみえますが、
あれも「結果的に」
生じた過渡応答です。)
その「過程」が現れる場所。
それが「伝送路」です。
伝送路上には、
反射波が往来します。
重ね合わせの原理により、
往来した反射波の和が、
伝送路上に現れる電圧となります。
反射波は、
伝送路の両端で、
常に決まった比率(反射係数)で、
反射します。
単純な回路で考察
伝送路上で、
反射波が重ね合わされる
様子について、
単純なモデルを
下図に示します。
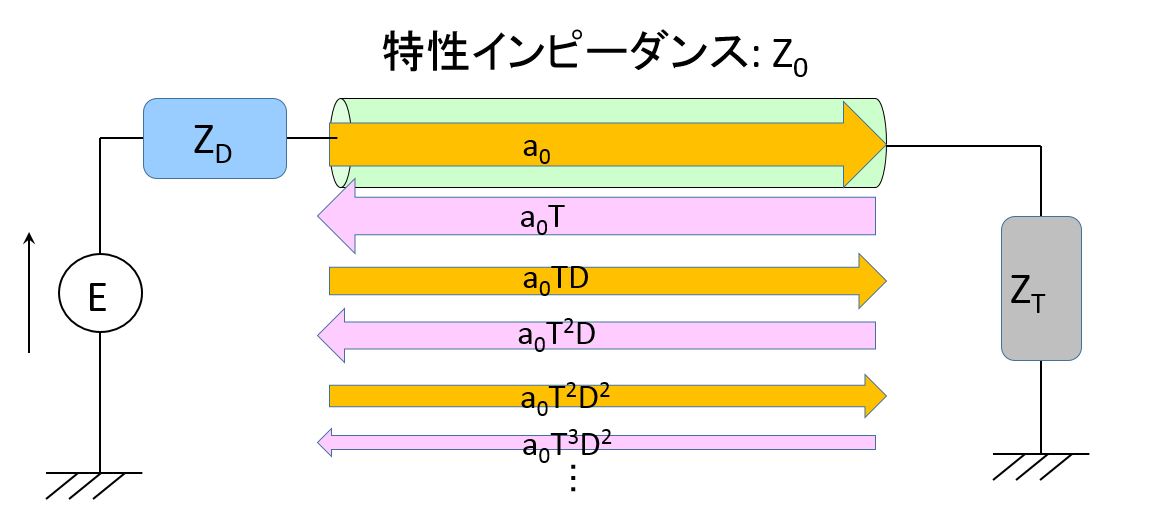
緑色の円筒を伝送路とし、
特性インピーダンス: $\ Z_{0}$
電源の入力インピーダンス: $\ Z_{D}$
終端のインピーダンス: $\ Z_{T}$
右側の反射係数: T,
左側の反射係数: D
とします。
オレンジの矢印は、
右から左へ進行する電圧の波動。
ピンクの矢印は、
左から右へ進行する電圧の波動です。
オレンジの矢印と、
ピンクの矢印は、
反射が起きるたびに
一つずつ増えていきます。
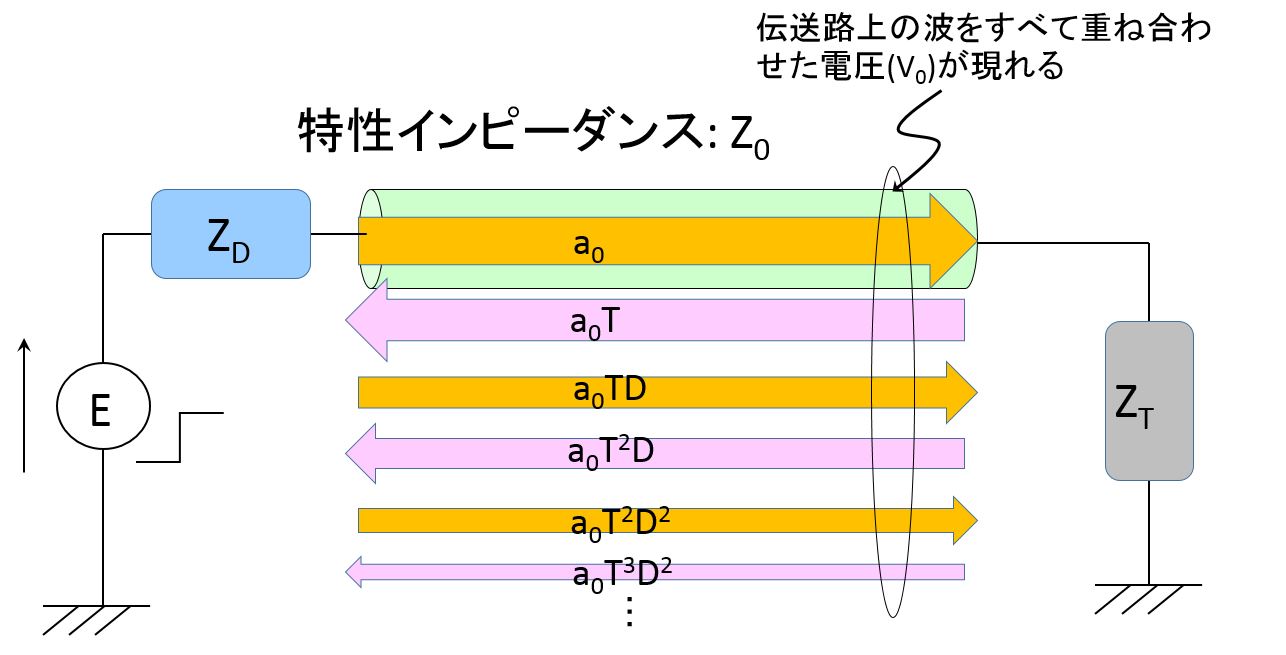
最終的に
伝送路上に現れる電圧: $\ V_{0}$
は、オレンジ矢印の電圧値と、
ピンク矢印の電圧値
すべての総和となります。
伝送路の両端では、
決まった反射係数で、
反射が起きるので、
オレンジとピンクの矢印の
ひとつひとつの電圧値は、
それぞれ、
無限等比級数となっているのが分かりますね。
オレンジ: 初期値が $\ a_{0}$,比: TD の無限等比級数
ピンク : 初期値が $\ a_{0}T$, 比: TD の無限等比級数
矢印の総和は、
ピンク矢印の無限等比級数の和と
オレンジ矢印の無限等比級数の和
を足したものとなります。
ここで、オレンジもピンクも、
無限等比級数の比:TDですね。
T, Dはそれぞれ、
(全反射の場合を除いて)1未満となりますので、
TD<1となります。
そのため、オレンジもピンクも、
無限等比級数の和は、
有限の値に収束します。
次回に続く


関連